1317. Дни рождения

Рожь. 1878. Пейзаж стал классическим и программным произведением, как для самого художника, так и для художественной критики его времени. На одном из эскизов к картине И.И. Шишкин сделал запись, которую можно считать его творческим кредо: «Раздолье, простор, угодье, рожь, Божья благодать, русское богатство».

Лирическое отношение к отечественной природе, воспетое И.И. Шишкиным, было ярко выражено в стихах Н.А. Некрасова:

Все рожь кругом, как степь живая,

Ни замков, ни морей, ни гор.

Спасибо, сторона родная,

За твой врачующий простор.

Известно, что в группе из 23 или более человек вероятность того, что хотя бы у двух из них дни рождения (число и месяц) совпадут, превышает 50%. Этот факт может показаться противоречащим здравому смыслу, так как вероятность одному родиться в определённый день года довольно мала, а вероятность того, что двое родились в конкретный день – ещё меньше, но является верным в соответствии с теорией вероятностей. Таким образом, факт не является парадоксом в строгом научном смысле – логического противоречия в нём нет, а парадокс заключается лишь в различиях между интуитивным восприятием ситуации человеком и результатами математического расчёта.

Для заданного количества людей вычислить вероятность того, что двое из них родились в один день года. Год считать равным 365 дням.

Вход. Каждая строка является отдельным тестом и содержит количество людей n (1 < n < 400).

Выход. Для каждого значения n в отдельной строке вывести вероятность того, что хотя бы у двух из n людей дни рождения (число и месяц) совпадают. Искомую вероятность выводить в процентах и округлять до 8 знаков после запятой как указано в примере.

Пример входа	Пример выхода
2 10 23 366	0.27397260% 11.69481777% 50.72972343% 100.00000000%

РЕШЕНИЕ

теория вероятности

Анализ алгоритма

Рассчитаем сначала, какова вероятность того, что в группе из n человек дни рождения всех людей будут различными. Если n > 365, то в силу принципа Дирихле вероятность равна нулю. Если же n ≤ 365, то будем рассуждать следующим образом. Возьмём наугад одного человека из группы и запомним его день рождения. Затем возьмём наугад второго человека, при этом вероятность того, что у него день рождения не совпадёт с днем рождения первого человека, равна 1 – 1/365. Затем возьмём третьего человека, при этом вероятность того, что его день рождения не совпадёт с днями рождения первых двух, равна 1 – 2/365. Рассуждая по аналогии, мы дойдём до последнего человека, для которого вероятность несовпадения его дня рождения со всеми предыдущими будет равна 1 – (n – 1) / 365. Перемножая все эти вероятности, получаем вероятность того, что все дни рождения в группе будут различными:

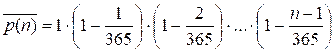
Тогда вероятность того, что хотя бы у двух человек из n дни рождения совпадут, равна

Реализация алгоритма

В ячейках p[i] будем запоминать значения вероятностей p(i).

double p[401];

Положим p[1] = 1. Остальные значения ячеек p[i] вычислим по формуле, указанной в анализе задачи.

p[1] = 1.0;

for(i = 2; i < 401; i++)

p[i] = p[i-1] * (1.0 - (i - 1.0) / 365);

Для каждого входного значения n выведем ответ.

while(scanf("%d",&n) == 1)

printf("%.8lf%%\n",(1 - p[n]) * 100);